Itt most nem szeretnék a GPS-es mérések elvéről értekezni, mert ez egyrészt nem egy könnyen emészthető téma - pláne, ha még bele is mélyedünk -, másrészt nincs is szükségünk most rá. Elég elfogadnunk azt a tényt, hogy van egy mobiltelefon nagyságu kütyü a kezünkben, ami valamilyen módszerrel képes arra, hogy a terepen meghatározza a pozíciónkat és ezt el tudja a memóriájába menteni. Ezért a következőkben inkább a mérési pontosságról mondanék pár érdekes dolgot, valamint elmagyaráznám, hogyan készültek a honlap ezen fejezetében található szintmetszetek és táblázatok. Ígérem, nem kell különösebb matematikai felkészültség az itt leírtak megértéséhez!
Ez nagyon fontos kérdés, jobb már a legelején tisztázni a dolgokat. Hiszen teljesen más adatokat találsz a pecsételő pontok közötti távolságról és szintekről a pecsételő füzetedben, mint mondjuk a Magyar Természetjáró Szövetség (MTSZ) hivatalos Országos Kéktúra oldalán, megint másokat itt, ezen a honlapon. Nem nagyon térnek el ezek az adatok egymástól, jó esetben csak néhány százalékot szórnak felfelé vagy lefelé, de mi ennek vajon az oka? A válasz nagyon egyszerű: több, különböző méréssel térképezték fel az Országos Kéktúra útvonalát, és ezek eltérnek egymástól. De vajon miért mérünk ugyanazon útvonalról más és más értékeket?
Ennek alapvetően két oka lehet:
- Megváltozott közben az útvonal, emiatt változtak meg a távolság- és szintadatok is. Ez a legegyszerűbb, legkönnyebben kezelhető dolog. Emiatt szerepel a honlapomon minden tájegység fejezetének tetején, hogy mikor is készítettem el a felmérést. Ez alapján készült el aztán a szintmetszet, és persze a táblázatok is. A pecsételő füzettel kissé más a helyzet. Ott nem szerepelnek a dátumok a felmérés időpontjáról, de a füzet kiadása évéből és a térképvázlatokból következtetni lehet erre. Az MTSZ honlapján még ennyi információ sincs, de mivel maga az oldal sem régi, fogadjuk el, hogy a felmérése sem lehet öregebb egy-két évesnél. Az útvonalváltozásból eredő eltérések azonban nem indokolják azt, mért tér el az ÖSSZES adat egymástól!
- A mérési- és feldolgozási hibák miatt térnek el egymástól az adatok. Ez a második pont már keményebb dolog, hiszen felmerülhet benned kedves Olvasóm, miért nem lehet végre egyszer pontosan megmérni az Országos Kéktúra útvonalát! Hiszen nem kell hozzá más, mint egy jó műszer és precíz adatfeldolgozás, és az abból képződött adatokat el lehetne fogadni afféle etalonnak! Sajnos, ez nem ilyen egyszerű dolog! Hogy ezt megérthesd, kicsit messziről kell indulnom, de ha kíváncsi vagy rá, mi az eltérések oka, olvasd el ezt a fejezetet!
Vegyünk egy sima deszkalapot és üssünk bele kalapáccsal két vékony szeget, nagyjából egy méternyi távolságra egymástól. A feladat az, hogy a lehető legpontosabban meghatározzuk a két szeg közötti távolságot, méghozzá azt a távolságot, amit a két szeget összekötő egyenes mentén mérnénk (vagyis a két szeg közötti legrövidebb távolságot). Sokfajta mérőeszközzel elvégezhetjük ezt, például a fiunk iskolai vonalzójával, vagy a feleségünk szabászcentiméterével, mi válasszunk egy, a lakásban általában fellelhető meglehetősen pontos eszközt, a barkács mérőszalagot. Illesszük oda a kezdetét az egyik szeghez, húzzuk ki a szalagot és ügyelve arra, hogy egyenes maradjon, olvassuk le az értéket a másik szegnél. Legyen az érték az egyszerűség kedvéért pontosan 1000 milliméter. Ennyi hát a távolság! Most már nyugodtan hátradőlhetünk: na, ezt a munkát is elvégeztük!
Aztán miközben a mérőszalaggal játszunk, észreveszünk egy jelzést a szalag elején: egy nagy római kettest! Ez az Európai Parlament által tett 2004/22/EG ajánlásra utal, ami a mérőeszközök pontossági osztályokba való sorolásáról intézkedik. És bizony, eszerint az ajánlás szerint a mérőszalagunk 1 méter hosszon akár fél millimétert is tévedhet! Hogy is van ez? Mérjük meg egy másik szalaggal a távolságot!
Elrohanunk a barkácsboltba, veszünk egy másik mérőszalagot, esetleg kölcsönkérjük a szomszédét, azzal is megmérjük a szögek távolságát, azzal meg csak 999,5 millimétert mérünk! Tévedhetnek ennyit a mérőszalagok? Hát persze! És azt sem tudjuk, melyik szalag a pontatlan: a miénk, a szomszédé, vagy esetleg mindkettő? Aztán közben rájövünk arra is, hogy nem mindegy, hogy olvassuk le a mérőszalagot, mert azzal is tévedhetünk! Helyben vagyunk hát! Felfedeztük a mérési pontosság két összetevőjét: mérőeszköz pontosságát, és a leolvasási pontosságot! Tehát fél millimétert tévedhet a mérőszalag, nagyjából mi is ennyit hozzátehetünk a leolvasási pontatlansággal - ha éppen nincs kéznél a nikkelezett szemmértékünk. Ebből adódik a mérési pontatlanság, ami jelen esetben 1 méterre vonatkoztatva 1 milliméter, vagyis 1 ezrelék.
Most két másik szeget üssük bele egy elvetemedett, göcsörtös deszkába is, és jelöljünk ki közöttük ceruzával egy nagyjából méteres, kacskaringós utat! Ennek a hosszát vajon milyen pontossággal tudnánk megmérni a korábbi mérőszalagunkkal? Nekilátunk és nehézkesen, pár centis szakaszok hosszának megmérésével és összegezésével aztán kapunk egy számot. De mennyire lehet az pontos? Mennyi lehet az eltérés a kanyargós vonal tényleges hosszától? Egy centiméter? Esetleg kettő? Azt hiszem, örülnénk, ha tudnánk, hogy 1 centi pontossággal mértük meg a vonal hosszát! 1 centiméter eltérés 1 méter hossza vetítve pedig egy százalék hibának felel meg.
Az Országos Kéktúra útvonala bizony meglehetősen „göcsörtös”, hepe-hupás, egyenetlen, ráadásul eléggé kanyargós is. Azt hiszem, itt is örülhetünk, ha az útvonal hosszát egy százalék pontossággal meg tudjuk mérni! A pecsételő füzetek legfrissebb kiadása szerint az útvonal 1162,1 km hosszú. Egy százalékos mérési pontosságot feltételezve pedig akár hosszabb vagy rövidebb is lehet ennél több mint 11 kilométerrel! Ezért van az, hogy minden felmérés eredménye más! Az én mérésem alapján az OKT hossza 1165,75 km-re adódott, ami azt jelzi, a két különböző mérés eltérése bőven belül van az 1%-on, nagyjából 0,3%. Mivel a méréseimet 2010 és 2011 folyamán végeztem, azóta kénytelen voltam az időközben történt útvonalváltozásokat bejárni és az adataimat frissíteni. Most a táblázatok és adatok a 2018 decemberi adatokat tartalmazzák.
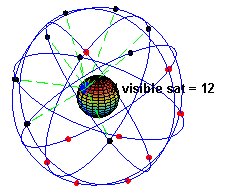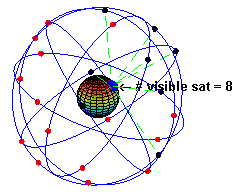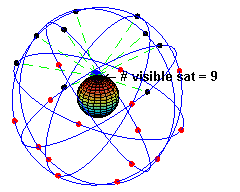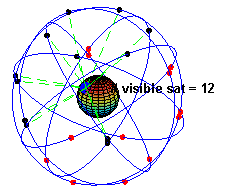
A GPS műholdak keringése a Föld körül

Garmin etrex Vista Hcx turista GPS. Egy ilyennel mértem fel az Országos Kéktúra útvonalát.
Találtam egy nagyon szép animációt arról, hogyan keringenek a GPS műholdak a Föld körül, és hogy a felszín egy pontján álló megfigyelő éppen mennyit látna belőlük a horizont felett, ha nagyon éles szemmel feltekintene az égre. De nem kell szemmel tartanunk a műholdakat, megteszi ezt helyettünk az a kis kütyü, amit egyszerűen csak GPS-nek hívunk. Ha legalább három műholdról kap jelet, akkor meg tudja határozni a földrajzi pozíciónkat. Minél többet lát belőlük (például nem takarják el őket hegyek, építmények, stb.), annál pontosabban mér, jó esetben körülbelül 2-3 méteres pontossággal megállapítja a pozíciónkat és rávetíti a kijelzőjén látható térképre. Ennyi tehát a mérőeszköz és a mérési elv pontatlansága. Ne felejtsük el, ez egy polgári célra „lebutított” eszköz, katonáék legalább egy nagyságrenddel pontosabban tudnak mérni vele!
A turista GPS a gépjármű navigációs készülékektől alapvetően különbözik abban is, hogy van egy olyan memóriája, amibe előre beállítható sűrűséggel elmenti az általa mért pozíciókat. Ezt a pontsort nevezik angolul track-nek (kiejtve: trek), ami magyarra fordítva nagyjából nyomot, nyomvonalat is jelenthet. És ez valóban az: ha a kütyüt a túra elején bekapcsoljuk és felakasztjuk mondjuk a hátizsákunk vállszíjára, akkor 10 másodperces mentési sűrűséget beállítva egy nyolcórás túrán képződik körülbelül 3000 pozícióadat, amit egy térképre rajzolva vagy elektronikusan rávetítve megjelenik az általunk megtett útvonal, tulajdonképpen maga a nyomvonalunk.
A turista GPS-ek persze a puszta földrajzi koordináták kijelzésén kívül a szintén a memóriájukban lévő térképre rá is vetítik a helyzetünket, ami a kijelzőjükön meg is nézhető, de göngyölt adatként közlik az általunk addig a pontig megtett távolságot, szintemelkedést és egyéb adatokat is. A távolságot úgy állapítja meg, hogy minden szomszédos mérési pont között kiszámolja a csupán néhány méteres távolságot (egy turista átlagos tempóval 1 másodperc alatt nagyjából 1 métert tesz meg), és ezeket az elemi távolság adatokat összegezi.
A magasságmérés már eltérő. Az egyszerűbb turista GPS-ek a magasságot is a műholdakról vett jelek segítségével számítják ki, a jobbak rendelkeznek úgynevezett barometrikus magasságmérővel. A legjobb GPS-ek azonban képesek a két magasságmérési módszert kombinálni, így csökkentve a mérési hibát a legkisebbre. Hogyan? Erről egy kicsit később fogok beszélni. A lényeg: a track adatai (a pontok földrajzi hosszúsági és szélességi adatai a hozzájuk rendelt magassággal és időadatokkal) le is menthetőek a számítógépre a GPS memóriájából.
Azt hiszem, épp itt az ideje, hogy arról is szóljak, hogyan jártam/járom végig az útvonalat. Mivel célom az, hogy a lehető legpontosabb adatokat közöljem itt a honlapon, ezért a lehető legpontosabban kell bejárnom az útvonalat is! Így aztán felállítottam néhány szabályt, amikhez maximálisan igyekszem tartani magam a kéktúra bejárás során.
- Első lépésként eldöntöttem, hogy csakis az Országos Kéktúra útvonalát mérem fel, vagyis a kék sáv jelzésekkel ellátott útvonalat járom be. Ez kissé triviálisan hangzik, de nem olyan egyszerű a dolog! Sajnos, a kéktúra igazolófüzet adatai sokszor nem egyértelműek, vagyis nem lehet tudni, hogy a távolságok tartalmazzák-e a pecsételőpontokhoz való letérést, avagy sem. Én egyértelműen kijelentem, hogy a szintmetszeteken és a fő táblázatokban csakis a kék sáv jelzés által bejárt útvonal szerepel, a pecsételőpontokhoz való letérés nem!
- Sajnos nem mehetek az utak közepén, hogy a középvonalukon mérjem végig az útvonalat. Ennek oka érthető: az utakon könnyen elsodorhatnának az autók. Ezért mindig az aszfalutak menetirány szerinti bal oldalán ballagok, szemben a forgalommal. A KRESZ szabályok is ezt írják elő. Földutakon, keréknyomokon általában a jobb oldalon szoktam menni - ne kérdezzétek, miért! Így szoktam meg. Az ösvényeken, turistautakon pedig középen szoktam haladni. Joggal merülhet fel a kérdés, hogy mi van akkor, ha az út bal szélén baktatok, de jobb oldalon vannak felfestve a jelzések? Országúton és földúton maradok a fentebb leírt oldalon, lakott területeken a festett oldal járdáin haladok (ha van járda).
- A felmérés során 10 másodpercre van állítva a GPS mérési sűrűsége, pontosabban ilyen gyakran menti az adatokat a memóriájába. Így elfér egy 3-4 napos túra a memóriájában, de a pontok sincsenek túl ritkásan. Éles kanyarokban, elágazásokban, ahol fordulnom kell, megállok egy kis időre a sarkon, és elszámolok magamban 15-ig, csak azután indulok tovább. Így biztosan fog esni egy mérési pont a fordulási pontra is.
- Menet közben a GPS a hátizsákom jobb vállszíjára van felfűzve, tehát nagyjából másfél méterre a talajtól. Így kicsivel jobb a jelek vétele - na nem azért, mert így közelebb van a kütyü a műholdakhoz, de így árnyékolok a legkevesebbet a testemmel. Ez elvileg a magasságmérésekbe belejátszik, de ilyen aprósággal azért nem foglalkozom!
Amikor aztán a túra végén hazaérkezem, kezdődhet az útvonal adatainak feldolgozása! Azért ez sem néhány perces munka: ökölszabályként elmondhatom, hogy nagyjából annyi időt töltök az adatok feldolgozásával, mint magával a túrával! Hogy miért? A későbbiekben erre is választ haphatsz, kedves Olvasóm!
De hát miért is kell feldolgoznunk az adatokat? A cél az, hogy a kirándulás adataiból szeretnénk egy kéktúra szakasz pontos track-jét felvenni. Tehát egy alkalmas szerkesztőprogrammal (ez az én esetemben a Garmin által a GPS-eihez kifejlesztett MapSource program) el kell távolítani a nyomvonalból a felesleges részeket: amikor letértünk az útvonalról egy pihenőhely padjaihoz, elsétáltunk a pecsételőponthoz, rácsatlakoztunk a túra elején az útvonalra és a végén letértünk róla, mondjuk a buszmegállóhoz, vagy éppen eltévedtünk és tévelyegtünk pár percet az erdőben, stb.
Azt se felejtsük el, hogy miközben ülünk az erdei pihenő padján, a GPS akkor is mér, és a pihenés közben mért pontokra is érvényes a mérési pontatlanság: vagyis a készülék egy helyben áll, de a mért pontok szórásából úgy látszik, mitha ugrálnánk, vagy legalábbis sétálgatnánk a pad körül, ami bizony megnöveli a mért távolságot, hiszen a készülék nem tudja, hogy állunk, ő csak adogatja össze rendületlenül a mért pontok közötti távolságot, ami persze csak a mérési hibából adódik!
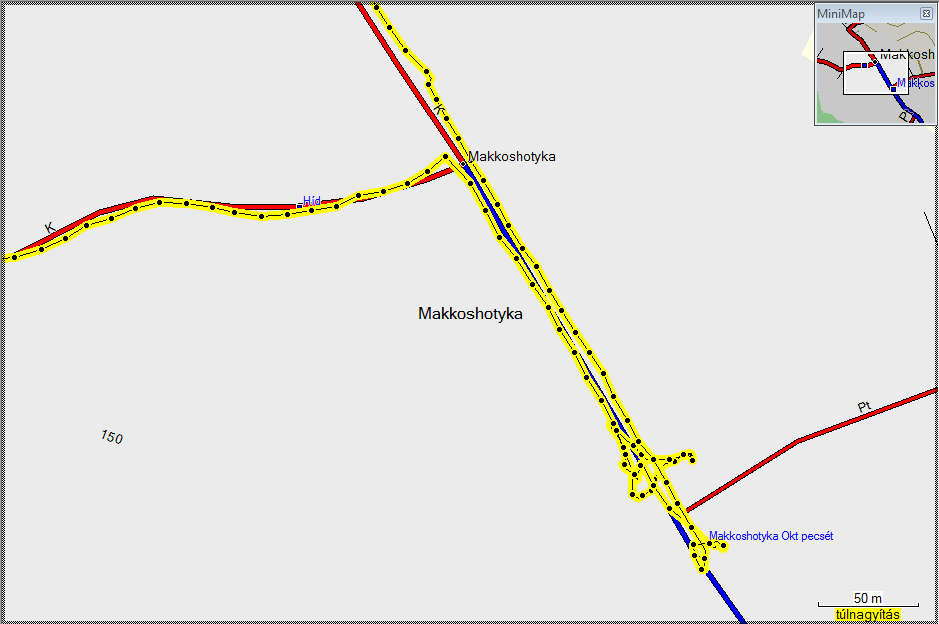
Hogyan jutottam el Makkoshotykán a boltba és a kocsmába? A képre kattintva az nagyobb méretben is megnyitható.
Ez nyomatékosan igaz a zárt helyekre: kocsmákra, boltokra, turistaházakra is. Ezeknél ráadásul az ablakokon keresztül csak kevés információt kap a GPS, tehát erősen szórnak a mérési eredményei is. Ezt is le kell műtenünk a track-ről. A végén nem marad más, csak az az útvonal, amit a kéktúra szakaszon tettünk meg. A képen jól látható a kéktúra útvonalról tett makkoshotykai kitérőm a boltba (fentebbi ponthalmaz) és a pecsételőhelyként is működő kocsmába (alsó ponthalmaz). Az oda- és visszaúton az utca két oldalán haladtam. Itt az egész kitérőt kimetszettem később a trackből, de a kocsmához vezető letérést később még figyelembe vettem a pecsételőpontokhoz vezető letérések hosszának számításánál.
A maradék adathalmazt átírtam egy egyszerű Excel táblázatba, ami szintén kiszámítja a szomszédos pontok közötti elemi távolságokat és összegezi azokat. A GPS a magasságot csak meghatározott minimális lépésekkel képes kezelni, ez az én készülékem esetén körülbelül fél méter. Ennél kisebb eltéréseket nem tud mérni. Az excel táblázat ezeket a magasságváltozásokat is összegezi, külön a szintemelkedést és lejtést. Elméletileg ez az adathalmaz már felhasználásra kész, az Excel tábla Diagram varázslójával kirajzolható a pontos szintmetszet.
Természetesen a táblázatban külön kiszámolható az egyes jellemző pontok közötti távolság és szintemelkedés is. Ezekből az adatokból készült az összesítő táblázat minden tájegységre vonatkozóan.
Készítettem egy egyszerű rajzot, azon szeretném ezt elmagyarázni. Nem kell semmilyen komoly matematikai előképzettség a megértéséhez, csak józan paraszti ész! A középső vízszintes vonal mutatja a tényleges útvonalat, a rajta lévő pöttyök azt, hogy mikor mért a GPS. A pontok körül lévő karikák a mérési bizonytalanságot jelölik, tehát azon a körön belül bárhová tehet minket a GPS. Könnyű belátni, ha előre, vagy hátrafelé tévedne csak a mérés, az könnyen kiegyenlítődne, hiszen amennyivel többet mérne két szomszédos pont közé az egyik helyen, annyival kevesebb lenne a táv a következő elemi szakaszon, tehát itt nincs összeadódó (kumulatív) hibáról szó.
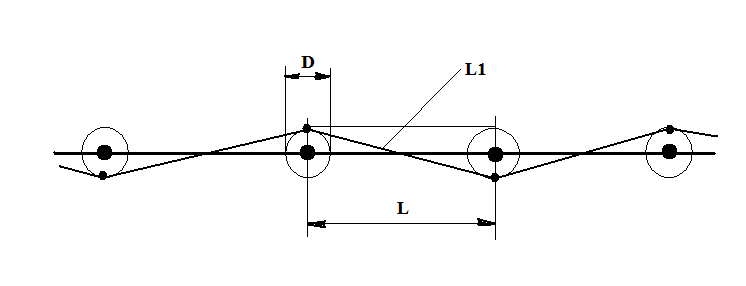
A GPS-alapú távolságmérés hibája.
Baj akkor van, ha az útvonal mellé „tesz” minket a kütyü. Megteheti? Szíve joga megvan hozzá! Lássuk hát a rajzot! „L” a két szomszédos pont közötti távolság, ez legyen 10 méter (Ez megfelel egy 3,6 km/h-s gyalogos sebességnek és 10 másodperces mérési időintervallumnak). A mérési pontatlanság, a kör sugara legyen 2 méter, tehát a „D” átmérő 4 méter. Tételezzük fel a legrosszabb esetet, vagyis azt, hogy az egyik mérésnél az út egyik oldalára tesz minket a maximális tévedéssel, aztán legközelebb pedig a másik oldalra. Lássuk hát, mennyinek mérte ezt a GPS!
A Pitagorasz-tétel segítségével kiszámíthatjuk, ha egy derékszögű háromszög két befogója „L” és „D” 10 és 4 méter (ki is rajzoltam a háromszöget), akkor az „L1” átfogója 10,77 méter! Vagyis 10 méteres távolságot 2 X 2 méteres oldaleltéréssel megmérve és maximális hibát feltételezve csupán 77 centit tévedtem (7,7%). És most a legrosszabbat tételeztem fel, ráadásul a GPS eléggé következetesen tud tévedni a valóságban, tehát inkább állandóan az útvonal bal, vagy jobb oldalára tesz, minthogy csak úgy össze-vissza mérne! Köszönjük szépen, Pitagorasz!
Mindenesetre az is kiderül a rajzból, hogy nem érdemes a mérési pontokat minden határon túl sűríteni, mert akkor a szomszédos pontok közötti távolságok már egy nagyságrendbe esnek a mérési hibával, extrém esetben a szomszédos pontok egymás szórási körén belül lesznek. Ez nagyon megnöveli a mérési hibát, ráadásul úgy, hogy a valóságosnál nagyobb távolságot mérünk a megtett útra. Azonban nem szabad belesnünk abba a hibába sem, hogy nagyon megritkítjuk a mérési pontokat. Bár így a kevesebb mérési pont esetén kevesebb az összhibánk egy egyenes úton, viszont nem tudjuk felmérni a kanyargós ösvények pontos hosszát, ugyanis a kiértékeléskor mindig a szomszédos pontok között húzott egyenes hosszát számoljuk ki (így tesz a GPS is), nem pedig a kanyarulat ívének hosszát. Némi kísérletezgetés végén jutottam arra a következtetésre, hogy a legjobb a percenkénti 4-6 mérés (10-15 másodpercenként). Mivel a GPS-ek útvonalmemóriája általában 10.000 pont - az enyémnél is ennyi -, egy három-négy napos túra teljes nyomvonala elfér még a memóriájában.
És még egy dolog, amiről nem feledkezhetünk meg! A GPS nem a tényleges földfelszínen számítja a mért pontok közti távolságot, hanem nagyjából a tengerszintnek megfelelő magasságban, egy képzeletbeli forgástesten (a pontos neve: forgási ellipszoid), ami jól modellezi a földgömb sarkokon kissé lapult, úgynevezett geoid alakját. Ez valamennyi hibát okozhat a távolságmérésben, hiszen nem a tényleges úthosszt mérem, hanem csak annak a vízszintes vetületét. Ide újra igaz a Pitagorasz törvény: a korábbi adatoknál maradva, ha 10 méteres távon 4 métert emelkedik vagy lejt az utam (és ez már elég erős turista kaptató!), akkor ténylegesen 10,77 métert teszek meg, de ebből csak a vízszintes vetület (a 10 méter) kerül rögzítésre.

Túrázás lejtőn és emelkedőn
Tehát távolságmérésnél kétfajta hiba léphet fel: a GPS mérési pontatlanságából adódó hiba növeli a megtett távolságot, az emlkedőn/lejtőn megtett utat viszont kevesebbnek mutatja. Mivel változatos, hegyes-dombos területen szoktunk általában túrázni, a két hibafajta egymás ellen hat, és ha nem is egyenlítik ki egymást, kétségtelen, hogy egy nagyságrendbe esnek és csökkentik a teljes mérési hibát.
A kísérlet kedvéért a Hűvösvölgy-Rozália téglagyár kéktúra szakaszt háromszor végigmértem, különböző időjárási körülmények között, kétszer odafelé és egyszer visszafelé, a legrövidebb és leghosszabb mérés különbsége 110 méter volt a nagyjából 14,1 km hosszú szakaszon, vagyis valamivel kevesebb, mint 1%. Ez azt hiszem, eléggé elfogadható. Joggal feltételezhetem, hogy a teljes Országos Kéktúrát ilyen pontatlansággal tudom végigmérni.
Itt meg kell különböztetnünk az abszolút és kumulativ (göngyölt, vagy összegezett) hibát. Az abszolút hiba az egyszerűbb, kezdjük hát azzal! Mivel a jobb GPS-ek a légnyomást mérik, az alapján számolják a magasságot egy igen egyszerű összefüggés alapján, miszerint minél magasabbra kapaszkodunk egy hegyen, annál kisebb lesz a minket körülvevő légnyomás, méghozzá nagyjából 1 kilométeres magasságig 9 méterenként 1 millibarral. Igen ám, de a légnyomás változó egy adott helyen is, hiszen függ a meteorológiai viszonyoktól, ezért szükségünk van egy pontos magasságértékre, amihez bekalibrálhatjuk a GPS-t a mérés kezdetén. Én meghatároztam a lakásunk tengerszint feletti magasságát, így aztán a konyhaablak párkányára helyezett kütyünek a túra reggelén, indulás előtt pontosan 185 méter tengerszint feletti magasságot kell mutatnia! Ha bekapcsoláskor nem ennyit mutat, akkor erre az értékre kalibrálom. Ekkor méterre pontos lesz a magasságmérés.
Lakásunk magasságának a megméréséhez egy nagyon egyszerű módszert választottam: nem kellett más, csak egy pontosan ismert magasságú hely. Minden magasabb hegy csúcsának tengerszint feletti magasságát méter pontossággal közlik a turistatérképek, én a Dobogókőt választottam ki erre a célra. Egy szép, napos nyári délelőtt fogtam magam, kocsiba ültem és felautókáztam a Dobogókő tetejére. Fenn a kilátóponton, aminek a tengerszint feletti magassága 699 méter (erről még egy emléktábla is van ott felszerelve), bekalibráltam a GPS-em erre a szintre, aztán beültem az autóba és egy óra alatt hazaértem vele. Otthon megnéztem, mennyit mutat, így adódott a 185 méteres szint a konyhánk ablakpárkányára. Ezt a mérést és kalibrálást bárki elvégezheti a saját GPS-ével, csak arra ügyeljen, hogy a mérések elvégzésekor a légnyomás stabil legyen, erre pedig a szélcsendes, napos idő a legalkalmasabb. Ha van otthon barométer, akkor olyan időt válasszunk ki, amikor biztos, hogy nem érkezik meteorológiai front, a barométer mutatója pedig áll, mint a cövek (egy nap alatt sem változik a légnyomás 2-3 millibarnál többet). De még így is igyekezzünk minél gyorsabban elvégezni a két mérést.
A helyzet azonban nem ilyen egyszerű, nem elég csak a túra elején kalibrálni a GPS-t, mert a túra közben is változhat a légnyomás, egy-egy frontos napon akár 5-10 millibarral is. Ez viszont 45-90 méter magasságmérési hibát okozhat, hiszen a GPS alapból nem tudhatja, mitől változott meg a légnyomás: attól, hogy felfelé vagy lefelé haladtam, vagy attól, hogy front érkezett? Szerencsére erre is van megoldás: az én GPS-em is korrigálni tudja a magassági adatokat a GPS rendszerből számolt magassággal. Ezt én csak bekapcsolásnál látom működni: A készülék üzembe helyezésekor az első pár percben a barometrikus adatokból számolt magasságot jelzi ki, aztán egyszer csak elkezd változni ez az érték, mert megérkezik a korrekció a GPS adatokból. Ha ez az adat is beáll, akkor kellene csak a fentebb már említett végső kalibrációt elvégeznem.
Én azonban ezt a funkciót kikapcsoltam, mert különösen szerencsés helyzetben vagyok, ugyanis a munkahelyemen van egy meteorológiai állomás, ami által mért adatokat (hőmérséklet, légnyomás, páratartalom) a központi adatnyilvántartó rendszer percenként archiválja. Tehát nincs más dolgom, mint túra után, amikor újra megyek dolgozni, lekérem az adatokat (pontosabban ez előző napok nyomásváltozási diagramját) és ez alapján korrigálom a mért magassági értékeket az excel táblában. Most mondhatod erre, hogy például a Cserehátban, ahová túrázni megyek, más lehet a légnyomás, mint Budapesten, pontosabban más függvény szerint változik az értéke, de ez van! A légnyomásváltozási tendenciák jól érvényesülnek az én módszeremben is.
És most lássuk a kumulatív hibát! Ez akkor okoz problémát, ha egy útvonal, vagy egy szakasza emelkedését, lejtését szeretném meghatározni. De vajon hogyan? A barometrikus magasságmérésű GPS-ek csak egy bizonyos felbontóképességgel képesek mérni, ez az én GPS-em esetében körülbelül 0,5 méter. Ez kismértékben függ a környezeti légnyomástól, de nem érdemes részletesebben foglalkozni vele.
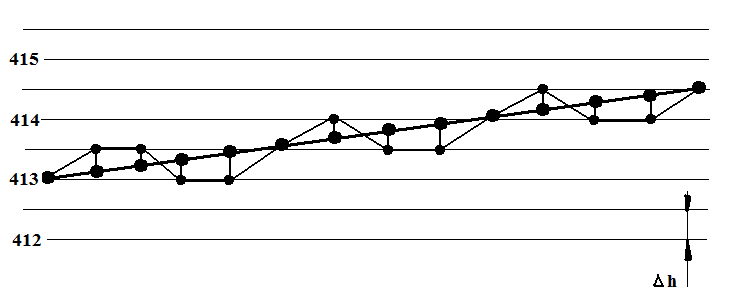
A GPS-alapú szintmérés hibája.
Az egyszerűség kedvéért tegyük fel, hogy minden egész és fél métert képes a kütyü kijelezni. A példában egy enyhe emelkedőn ballagok felfelé. Azt várhatnánk, hogy a magasságváltozást úgy jelzi majd ki, hogy 413 - 413 - 413 - 413 - 413,5 - 413,5 - 413,5 - 413,5 - 413,5 - 414 - 414 - 414 - 414 - 414 - 414,5. Tehát szépen, lépcsőzetesen. Ha a magasságváltozás háromszor fél méter, akkor a mérés elejétől a végéig 1,5 métert emelkedtem. Ez pontosan megegyezik a tényleges magasságváltozással, hiszen 413 méterről kapaszkodtam fel 414,5 méterre.
Sajnos a GPS nem így mér, hiszen már tisztáztuk a legelején, neki is joga van tévedni, ezért mondjuk a következő mérési sort rögzítette: 413 - 413,5 - 413,5 - 413 - 413 - 413,5 - 414 - 413,5 - 413,5 - 414 - 414,5 -414 - 414 - 414,5; ahogy a rajzon is látható. A kezdő- és végérték között megvan a másfél méter különbség, na de közben! Hat egységugrást mért felfelé és hármat lefelé. Vagyis úgy néz ki, mintha három métert (hatszor felet) kapaszkodtam volna felfelé, miközben ereszkedtem is lefelé másfelet (háromszor felet)! Ez bizony csúnya eltérés! És ez a fajta hiba okozza azt, hogy a különböző szintmérésekben sokkal nagyobbak az eltérések, mint a távolságmérésben!
Persze ez ellen lehet védekezni, léteznek különféle segédprogramok, amik igyekeznek valami átlagot vonni a mért adatokból, elsimítani a magasságeltéréseket, na de mindig fennáll a veszélye annak, hogy TÉNYLEG ilyen volt a terep, és a GPS a valóságot mérte! Ezért én ezeket a programokat nem használom, helyette egy kicsit gondolkodni kezdtem és kidolgoztam egy egyszerűsítő elvet.
Mintaként a 81-es főút és a Csókakő vára alatti parkoló közötti nagyjából 3 kilométeres, monoton emelkedő aszfaltos túraszakaszt használtam. Rájöttem, hogy az egységnyi felfelé-lefelé eltérések - amik a mérési hibákból adódnak - párba állíthatók, a párok pedig kölcsönösen kiejtik egymást, a végén nem marad más, mint csak a valóságos szinteltérés! Példánkhoz visszatérve, ha levonom a három pozitív-negatív párost, csupán a három plusz félméteres szintemelkedés marad, ami már megfelel a valóságnak! Ezt a módszert csakis az aszfaltúton haladó szakaszokra alkalmaztam, illetve oda, ahol tudtam, hogy egyhangú, enyhe emelkedőn, lejtőn haladtam a túra során.
Azért a probléma nem olyan súlyos, hiszen a hosszú, erős emelkedők, lejtők esetében nincs vita, mert ott a GPS is monoton emelkedést, süllyedést mér. Miért is? Ha a 10 másodperces mérési ciklusban két mérés között megteszek 10 métert vízszintesen, akkor egy 10%-os emelkedőn (ami turista fogalmak szerint eléggé enyhe) ehhez 1 méter magasságváltozás tartozik. Így aztán lehet, hogy két mérési pont között egyszer másfél méter szintet fog mérni, egy következőnél pedig csak felet, de már nincs emelkedés-lejtés, ami a mérést meghamisítaná.
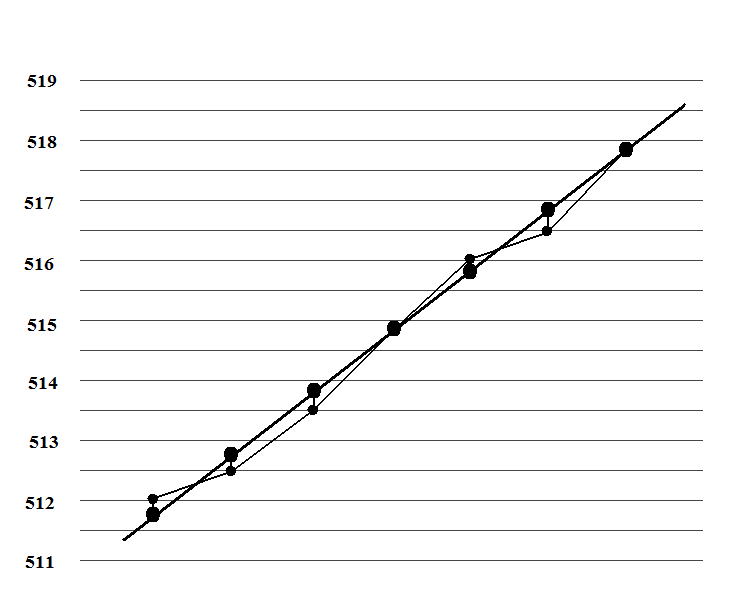
A GPS-alapú szintmérés hibája.
És itt kanyarodnék vissza a turista GPS-ek korábbi nemzedékéhez, amik még műholdas adatokból mérték a magasságot. Ezeknél bizony elég silány volt a magasságmérés pontossága, mert elvi okokból pontatlanabbul méri a készülék a magasságot, mint a földrajzi hosszúságot és szélességet. Persze ezek segítségével is meg lehet tudni pár méter pontossággal, milyen magasságban járunk éppen, a hatalmas pontatlanság csupán a gyűjtött, göngyölített adatoknál jelentkezik.
És végül egy zárógondolat:
Most, miután végigolvastad az egész fejezetet, kedves Olvasóm, gondolom már Te is rájöttél arra, hogy a kéktúra lehet hosszabb, vagy rövidebb annál, amit én mértem, de hogy nem pont olyan hosszú, az tuti biztos! No de a tréfát félretéve és komolyra fordítva a szót, én abban is biztos vagyok, hogy a távolságadatok plusz/mínusz 0,5 %-on belül vannak, tehát az Országos Kéktúra teljes hosszánál a tévedésem legfeljebb 5,5 km felfelé vagy lefelé, a résztávoknál persze arányosan kevesebb. A magasságmérés ennél jóval bizonytalanabb, itt a hibát plusz/mínusz 5 %-ra taksálom. Légy szíves, ezek figyelembevételével kezeld az adatokat! És még valami: én le merem írni azt, hogy mennyit tévedhettem a mérés és a feldolgozás közben. Másnál ilyet nem találsz.
Azt hiszem, a GPS-szel történő távolság- és szintméréssel kapcsolatban minden lényeges dolgot megemlítettem. Sajnos, ebben a témában én is csak laikus vagyok, de ha bármilyen kérdésed van, kedves Olvasóm, keressél meg egy e-mailban! Amennyiben tudok, válaszolok a kérdésedre!
- hörpölin -
| A tárhelyszolgáltató neve: | Port Kft. |
| A tárhelyszolgáltató címe: | 9200 Mosonmagyaróvár, Szent István király út 60. |
| A tárhelyszolgáltató e-mail címe: | info@webtar.hu |
| A honlap szerkesztőjének neve: | Horváth Béla |
| A honlap szerkesztőjének e-mail címe: | horvabe1959@gmail.com |
| A honlap szerkesztője mindent megtesz azért, hogy az itt közölt információk pontosak, frissek és teljesek legyenek, de semmiféle felelősséget nem vállal bármely, ezen információk használatából adódó kár bekövetkeztéért. A honlap adatainak használatával Ön elismeri, hogy azt csak és kizárólag saját felelősségére teszi. | |
 Creative Commons license: Attribution-NonCommercial-NoDerivatives 4.0 International Creative Commons license: Attribution-NonCommercial-NoDerivatives 4.0 International | |
| Kérem, olvassa el a honlap Cookie Policy-jét! Fontos információkat tartalmaz! | |
